تفهيم حساس IMU: نُظم تمثيل اتجاهية الجسم وربط قيم الحساس مع مكتبة VPython ثلاثية الأبعاد

طالعنا في المقالة السابقة مبدأ عمل حساسي التسارع والجايروسكوب داخل حساس الـIMU ، وتعرفنا على ميزات كل منهما، واستخلصنا قوانين حساب الزوايا الثلاث الإمالة pitch والدحرجة roll والانعراج yaw ، وثم استعرضنا كيفية تحسين ممانعة الإشارات المستخلصة من الضجيج، وفي مقالة أخرى، تحدثنا عن الحساس المغناطيسي وكيفية معايرته للحصول على زاوية البوصلة azimuth. في هذه المقالة، نطالع الأطر frames of reference المستخدمة في حساس الـIMU وتحديداً الإطار العطالي inertial frame وإطار الجسم body frame وهما الإطاران الأكثر شهرةً، ومن ثم نناقش محدودية استخدام الزوايا الثلاث لتمثيل النظام عند الزاوية 90 درجة وهذا ما يسمى بظاهرة Gimbal-lock، ومن ثم نتكلم عن معالجة ذلك باستخدام نظم تمثيل أخرى وهي axis-angle و نظام الكواتيرنيون Quaternion، وختاماً نقوم بتمثيل الدارة في الفضاء ثلاثي الأبعاد باستخدام مكتبة Vpython.

الأُطر المستخدمة في التعامل مع حساس الـIMU

إن قيم إحداثيات أي نقطة تتبع لإطار مرجعي frame of reference (محاور إحداثيات) معين ويكون الإطار المرجعي نسبي. إن أحد أهم الإطارات المستخدمة في حساس الـ IMU هو الإطار العطالي inertial frame وهو ثابت على سطح الأرض وإطار الجسم body frame وهو إطار متطابق مع جسم الحساس. نحتاج لإطارات وسيطة عند الحاجة للتحويل من الإطار العطالي إلى إطار الجسم وهي الإطارين vehicle-1 و vehicle-2. يوجد أُطر أخرى مستخدمة ولكن نكتفي بذكرالإطارين الأساسيين العطالي وإطار الجسم.

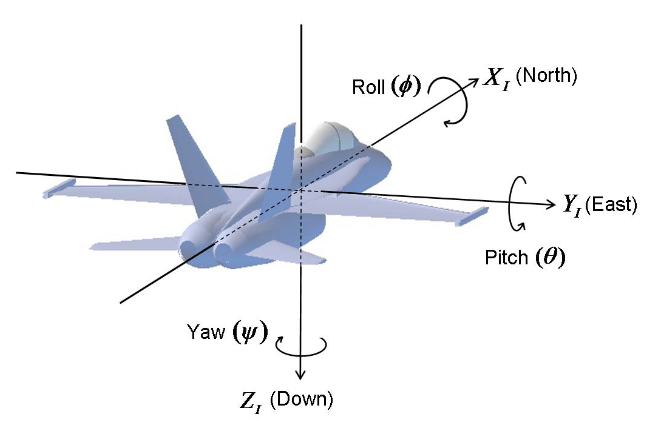
إن الإطار العطالي ثابت غير متحرك يكون فيه المحور x بجهة الشمال والمحور y بجهة الشرق والمحور z بجهة الجاذبية

لنفترض أن الطائرة انزاحت عن الشمال بزاوية انعراج Yaw، إن هذا الانعراج سيؤثر على المحورين x و y كما في الشكل أدناه

لتحويل شعاع من الإطار العطالي إلى الإطار vehicle-1 نستخدم مصفوفة التحويل. إن مصفوفة التحويل rotation matrix هي المصفوفة الحاصل جدائها بقيم الشعاع في الإطار العطالي تساوي فيم ذات الشعاع ولكن بالنسبة للإطار الجديد. 

يمكن استنتاج مصفوقة التحويل باستخدام قوانين المثلثات وتم ذكرها في الصورة التوضيحية أدناه:

يمكن تعميم المصفوفة الموضحة في الشكل السابق على فضاء ثلاثي الأبعاد إذ أن زاوية الانعراج لا تسبب تغير في المحور z وبهذا تكون المصفوفة 

إن الإطار vehicle-2 ينتج عن زاوية الإمالة عن الإطار vehicle-1 وإن مصفوفة التحويل تتميز هذه المرة بأنها ثابتة عند المحور y لأن الإمالة تكون بالدوران على المحور y. 

للوصول لإطار الجسم Body frame نضيف زاوية الدحرجة التي تكون حول المحور X ولذلك إن مصفوفة التحويل هذه المرّة ثابتة على محور X. 

يمكن التعبير عن مصفوفة التحويل من الإطار العطالي إلى إطار الجسم بالطريقة التالية: 

هل تمثيل معلومات التوجيه بالزوايا الثلاث كافي ؟

إن صيغة أويلر  Euler angles  هي تعبير عن حالة توجيه الجسم . يفشل هذا التمثيل عندما تقترب زاوية الإمالة من 90 درجة وتعرف هذه الظاهرة بـ Gimbal Lock ويمكن إثباتها رياضياً ولكن لن نتبحّر في تفصيلها هذه المرة ويكفي معرفة أن هذه الظاهرة تعني خسارة واحدة من درجات الحريّة الثلاث للنظام عند الزاوية 90 درجة. يمكن الاطلاع على المراجع لشرح وافي عن هذه الظاهرة.  بسبب هذه المحدودية يُستخدم التمثيل بالكواتيرنيون Quaternion التي سنشرح لاحقاً والذي لا يعاني من ظاهرة Gimbal Lock .

يجب التنبيه أن حركة الجسم في تمثيل أويلر يتم عبر سلسلة من الحركات عبر المحاور الثلاثة (الإمالة – الدحرجة – الانعراج)، وهذا طبعاً من الناحية الرياضية وليس كحركة فيزيائية إذا فعلياً نحرك الجسم بحرية مطلقة بالهواء، ولكن النموذج الرياضي الذي اشتققنا منه معادلات المقالة السابقة معتمد على وجود سلسلة من الحركات المتتابعة والمرتّبة. 

للتخلص من ظاهرة الـ Gimbal Lock نعتمد على نموذج تتم فيه الحركة دفعة واحدة بافتراض شعاع وزاوية دوران حول هذا الشعاع. 

إن  Axis-angle representation هو تمثيل بديل عن تمثيل زوايا التوجيه الثلاث، ويعتمد هذا التمثيل البديل عن شعاع يمثل توجه الجسم في الفضاء الثلاثي بالإضافة إلى زاوية تمثيل زاوية الجسم حول هذا الشعاع. نستطيع التحويل من تمثيل axis-angle إلى الكواتيرنيون كما سنشرح في الفقرة التالية.

التمثيل بالكواتيرنيون Quaternion

إن الكواتيرنيون هو تمثيل بديل عن تمثيل أويلر المتمثلة بالزوايا الثلاث: الإمالة والدحرجة والانعراج. يمكن التبديل بين نظامي التمثيل باستخدام صيغ رياضية محددة سنذكرها. إن الكواتيرنيون هو شعاع مكون من أربعة أرقام، 3 منها أرقام تخيلية ورقم حقيقي يعبر عن طويلة الشعاع.

للتحويل من axis-angle إلى الكواتيرنيون نستخدم الصيغة التالية، مع ملاحظة أن مركبات شعاع الدوران موضّحة في الشكل السابق: 

لتحويل شعاع من الإطار العطالي إلى إطار الجسم فإننا نستخدم المعالدلة التالية: 

نلاحظ أننا أضفنا عنصر صفر لشعاع الدوران في الإطار العطالي داخل معادلة التحويل، ويجب معرفة أن عملية الضرب في  الكواتيرنيون من أجل كواتيرنيون أول وثاني هي: 

إن مقلوب الكواتيرنيون conjugate هو ناتج قلب إشارة عناصره التخيلية فقط

 نلاحظ أننا نحتاج أن نقوم بعملتي ضرب، ولكن يمكن استخدام وبناء مصفوفة تحويل مباشرة وهي: 

ويكون التحويل بالشكل: 

للحصول على زوايا التوجيه الثلاث من الكواتيرنيون نستخدم المعادلات الثالث التالية: 

تمثيل الدارة عبر الـ VPython 

سنستخدم مكتبة Vpython لعرض سطح الدارة وتمثيلها في الفضاء ثلاثي الأبعاد، ولتمثيل السطح الذي يتموضع عليه الحساس IMU فإننا نعبر عنه بشعاع يصل بين نقطة الصفر في الفضاء الثلاثي (نقطة التقاء المحاور) ونقطة ذات إحداثيات x,y,z. لحساب هذه النقاط الثلاثة نبدأ من الزوايا الثلاثة المحسوبة عبر الحساس وهي زوايا الإمالة والدحرجة والانعراج. إن زاوية الانعراج تتشكل بين المحور x ومسقط شعاع الممثل للجسم على السطح XY وإن مطال هذا المسقط هو h. وباستخدام قوانين المثلثات نجد أن: 

سنفترض أن مطال شعاع السطح h هو واحدي.

ويبقى الإحداثية الثالثة z 

وبالمجمل 

ملاحظة: إن أسهم الإحداثيات في مكتبة VPython موضحة في الأسفل، ونلاحظ أن محور y يحل محل محور z في التمثيل الذي اعتمدناه، ولهذا تبقى حسابات الشكل السابق صحيحة ولكن فقط نعكس بين قيم z و y .

إن الكود المرجعي المستخدم لربط قيم الحساس مع توجيه الشكل ثلاثي الأبعاد معتمد على برنامج مكتوب في سلسلة دروس paul mcwhorterعن حساس الـ IMU وتحديداً الدرس الثامن عشر. تم إضافة تعديل وهو تعيين صورة لوجه الجسم الثلاثي الأبعاد. إن الكود الأصلي يعتمد على رسم أشكال ثلاثية الأبعاد تقريبية تعبيراً عن الدارة، ولكن وجدت أن الأكثر تعبيراً هو إضافة صورة لها على سطح المجسم ثلاثي الأبعاد. ولسبب ما فإن مكتبة Vpython لا تسمع بتعيين صورة للجسم إلا على الجوانب، ولحل هذه المشكلة عينت الصورة على الجانب الأيمن وأدرت الجسم بزاوية 90 درجة وهذا ما يفسر السطرين التاليين:

bBoard=box(texture={'file':'board.jpg','place':['right'] },length=.2,width=2,height=6,opacity=.8)
bBoard.rotate(angle=np.pi/2,axis=vector(0,0,1))

يرجى مراجعة الشكل السابق لمعرفة ترتيب المحاور والأبعاد في بيئة Vpython. سنعين ثلاث محاور ثابتة في الشكل تعبر عن محاور البيئة بالألوان (أحمر:x أخصر:y أزرق:z)

xarrow=arrow(lenght=2, shaftwidth=.1, color=color.red,axis=vector(1,0,0))
yarrow=arrow(lenght=2, shaftwidth=.1, color=color.green,axis=vector(0,1,0))
zarrow=arrow(lenght=4, shaftwidth=.1, color=color.blue,axis=vector(0,0,1))
 

وسنضيف محاور ثلاثة أخرى منطبقة على حسم الدارة وسنقوم بتحريكها لاحقاً في البرنامج 

frontArrow=arrow(length=4,shaftwidth=.1,color=color.purple,axis=vector(1,0,0))
upArrow=arrow(length=1,shaftwidth=.1,color=color.magenta,axis=vector(0,1,0))
sideArrow=arrow(length=2,shaftwidth=.1,color=color.orange,axis=vector(0,0,1))

نستخلص من الزوايا الثلاث المستقبلة عبر الاتصال التسلسلي الشعاع المعبر عن محور الجسم 

	body_x,body_y,body_z = cos(yaw)*cos(pitch),sin(pitch),sin(yaw)*cos(pitch)

نسمي هذا الشعاع بـ axis vector كما تسميه المكتبة 

	k=vector(body_x,body_y,body_z)

وللتعبير عن الجسم بمحاور ثلاث متعامدة منطبقة على الجسم وتتحرك حسب حركة الجسم فلابد من إيجاد المحورين المتعامدين مع الشعاع K أو axis vector وذلك يتم رياضياً عبر الجداء الشعاعي cross product  للشعاع k مع شعاع وسيط مؤقت وهو شعاع على محور y  

	k=vector(body_x,body_y,body_z)
	y=vector(0,1,0)
	s=cross(k,y)
	v=cross(s,k)

إن اشتقاقنا لمعادلات حساب مركبات الشعاع x,y,z لن تتغير إذا تغيرت زاوية الدحرجة، يمكن ملاحظة أن المركبات تم حسابها باستخدام زاوية الميلان والانعراج، ولهذا نستخدم صيغة دوران رودريغوس Rodrigues rotation formula والتي نستخدمها لحساب مركبات الشعاع الجديدة بعد الدحرجة.

إن صيغة رودريغوس تنص على وجود شعاع v في الفضاء الحقيقي ثلاثي الأبعاد وهذا الشعاع يدور حول شعاع واحدي k بزاوية theta بحسب قاعد اليد اليمنى. لإسقاط ذلك على مسألتنا، فإن زاوية الدوران في الصيغة هي زاوية الدحرجة وإن الشعاع v هو الشعاع المعبر عن up vectpr في مكتبة Vpython والشعاع k هو الشعاع axis vector. مع ملاحظة أن الشعاعين v و k متعامدين وبالتالي جداؤهم الداخلي inner product يساوي الصفر وبالتالي نحذف المركبة الأخيرة من صيغة ردوريغوس 

ومع حذف المركبة الأخيرة يتبقى من الصيغة: 

وهذا ما نجده في برنامج البايثون

vrot=v*cos(roll)+cross(k,v)*sin(roll)

ونعين أشعة الدارة في Vpython بهذا الشكل 

	bBoard.axis=vrot
	bBoard.up=k

نعين أيضاً الأشعة المنطبقة على جسم الدارة والتي استخلصناها عبر أجداء الأشعة سابقاً 

	frontArrow.axis=k
	sideArrow.axis=cross(k,vrot)
	upArrow.axis=v

يجب تعديل رقم المنفذ في الكود قبل تشغيله

from vpython import *
from time import *
from visual import *
import numpy as np
import math
import serial


ad=serial.Serial('/dev/ttyACM0',115200)
sleep(1)

canvas(title='IMU Data 3D Visualization', caption='A caption')

scene.range=5
toRad=2*np.pi/360
toDeg=1/toRad
scene.forward=vector(-1,-1,-1)

scene.width=800
scene.height=800

xarrow=arrow(lenght=2, shaftwidth=.1, color=color.red,axis=vector(1,0,0))
yarrow=arrow(lenght=2, shaftwidth=.1, color=color.green,axis=vector(0,1,0))
zarrow=arrow(lenght=4, shaftwidth=.1, color=color.blue,axis=vector(0,0,1))

frontArrow=arrow(length=4,shaftwidth=.1,color=color.purple,axis=vector(1,0,0))
upArrow=arrow(length=1,shaftwidth=.1,color=color.magenta,axis=vector(0,1,0))
sideArrow=arrow(length=2,shaftwidth=.1,color=color.orange,axis=vector(0,0,1))

bBoard=box(texture={'file':'board.jpg','place':['right'] },length=.2,width=2,height=6,opacity=.8)
bBoard.rotate(angle=np.pi/2,axis=vector(0,0,1))

while (True):
    while (ad.inWaiting()==0):
        pass
    roll,pitch,yaw= .0,.0,.0     
    try:
            dataPacket=ad.readline()
            dataPacket=str(dataPacket,'utf-8')
            splitPacket=dataPacket.split(",")
            roll=float(splitPacket[1])*toRad
            pitch=float(splitPacket[0])*toRad
            yaw=float(splitPacket[2])*toRad+np.pi
            yaw = -yaw
    except:
        pass
    log = 'Roll={},Pitch={},Yaw={}'.format(roll*toDeg, pitch*toDeg,yaw*toDeg)
    print(log)
    scene.caption = log
     
    rate(50)

    body_x,body_y,body_z = cos(yaw)*cos(pitch),sin(pitch),sin(yaw)*cos(pitch)
    k=vector(body_x,body_y,body_z)

    y=vector(0,1,0)
    s=cross(k,y)
    v=cross(s,k)
    vrot=v*cos(roll)+cross(k,v)*sin(roll)

    frontArrow.axis=k
    sideArrow.axis=cross(k,vrot)
    upArrow.axis=v
    bBoard.axis=vrot
    bBoard.up=k
    sideArrow.length=2
    frontArrow.length=4
    upArrow.length=1
    bBoard.width = 2
    bBoard.height = 6
    bBoard.length = .2

مراجع

• 9-Axis IMU LESSON 18: Visualizing Pitch and Yaw in Vpython by toptechboy.com.
• The Rotation Matrix – DoctorPhys
• CH Robotics – AN-1005 Understanding Euler Angles
• wang-yimu website – Gimbal lock.
• Gimbal-lock – Wikipedia.
• CH Robotics AN-1006 – Understanding Quaternions
• Mbedded.ninja blog – Quaternions.
• EE 267 Virtual Reality – Lecture 10.
• Axis-angle – Wikipedia.
• Virtual Reality course by Prof Steven LaValle – axis-angle representation.
• Quaternions for Orientation article by Pete Scheidler.
• VPython – Visual Python tutorial.